Hãy xem toán tiếng anh lớp 7 có khó không nào

Chúng ta hãy cùng xem toán tiếng anh có khó không nào các bạn.

Câu 1: Khoảng cách lớn nhất

A courier company has motorbikes that can travel km starting with a full tank. Two courier, Anna and Brian, set off from the depot together to deliver a letter to Connor’s house. The only refuelling is when they stop for Anna to transfer some fuel from her tank to Brian’s tank. She then returns to the depot while Brian keeps going, delivers the letter and returns to the depot. What is the greatest distance that Connor’s house could be from the depot?

[Lời dịch]    Một công ty chuyển phát nhanh có xe máy có thể di chuyển 300km với một bình xăng đầy. Hai người đưa thư, Anna và Brian, cùng nhau rời khỏi kho để gửi thư đến nhà Connor. Việc tiếp nhiên liệu duy nhất là khi họ dừng lại để Anna chuyển một ít nhiên liệu từ xe của cô sang xe của Brian. Sau đó, cô quay trở lại kho hàng trong khi Brian tiếp tục gửi thư và trở về kho. Khoảng cách lớn nhất có thể từ nhà Connor đến kho là bao nhiêu?

Hướng dẫn giải.

Gọi  a km  là khoảng cách từ kho đến địa điểm chuyển xăng từ xe của Anna sang xe của Brian. Khi đó quãng đường di chuyển của xe của Anna là  2a km  (cả đi và về). Quãng đường đi thêm được của Brian (nhờ việc chuyển xăng) không lớn hơn  a km.

Để khoảng cách từ nhà Connor đến kho là lớn nhất, thì Anna và Brian phải di chuyển tổng cộng  600 km (vừa hết xăng), và quãng đường Brian đi được là tối đa, nghĩa là quãng đường đi thêm được của Brian (nhờ việc chuyển xăng) là  a km.

Khi đó, Anna đã di chuyển quãng đường là 2a km còn Brian đi được  (300 + a) km.

Suy ra  3a + 300 = 600 <=> a = 100 km.

Khoảng cách lớn nhất có thể từ nhà Connor đến kho là   (300 + 100)/2 = 200 km.

Câu 2: Gạch hình thoi

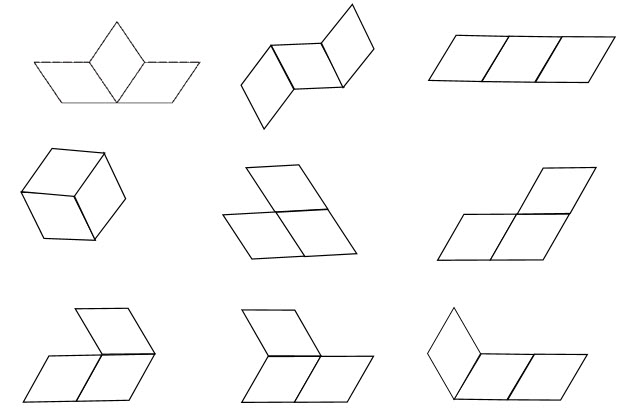
A rhombus-shaped tile is formed by joining two equilateral triangles together. Three of these tiles are combined edge to edge to form a variety of shapes as in the example given

How many diferent shapes can be formed? (Shapes which are reflectinons or rota-tions of other shapes are not considered diferent)

 [Lời dịch]  Một viên gạch hình thoi được tạo thành bằng cách ghép hai tam giác đều. Ba viên gạch như vậy khi ghép các cạnh với nhau sẽ tạo nên rất nhiều hình như ví dụ. Có bao nhiêu hình vẽ khác nhau được tạo thành (Các hình tạo thành bằng cách lấy đối xứng một hình đã có hay quay một hình đã có không được tính là hình khác biệt).

Hướng dẫn giải:

Có thể vẽ được 9 hình như sau:

Câu 3: Cắt giấy

Warren has a strip of paper 10 metres long. He wishes to cut from it as many pieces as possible, not necessarily using all the paper, with each piece of paper a whole number of centimetres long. The second piece must be 10 cm longer than the first, the third 10 cm longer than the second and so on. What is the length, in centimetres, of the largest possible piece?

[Lời dịch]        Warren có một mảnh giấy dài 10 mét. Cậu ấy muốn cắt mảnh giấy đó thành nhiều đoạn nhỏ nhất có thể sao cho độ dài mỗi đoạn là một số tự nhiên và không nhất thiết phải sử dụng hết toàn bộ mảnh giấy. Đoạn thứ hai cắt phải dài hơn đoạn đầu tiên 10 cm, đoạn thứ ba cũng dài hơn đoạn thứ hai 10 cm và cứ như vậy cho đến hết. Hỏi đoạn dài nhất mà Warren cắt được là bao nhiêu cm?

Hướng dẫn giải.

Ta thực hiện các bước giới hạn giá trị, ta chia được mảnh giấy ban đầu thành 14 mảnh có độ dài lần lượt là 1; 11 ; 21 ; … ; 131.

Ta có 1 + 11 + 21 + 31 + … + 131 = 924.

Nhận thấy 1000 – 924 = 76  và 76 : 14 = 5R6 nên mỗi đoạn giấy nhỏ ta có thể tăng thêm 5 đơn vị.

Vậy ta có 6 + 16 + 26 + 36 + … + 136 = 994.

Vậy đoạn giấy dài nhất mà Warren cắt được là 136 cm.

Câu 4: Số Terryfy

Terry has invented a new way to extend lists of numbers. To Terryfy a list such as [1, 8] he creates two lists [2, 9] and [3, 10] where each term is one more than the corresponding term in the previous list, and then joins the three lists together to give [1, 8, 2, 9, 3, 10] . If he starts with a list containing one number [0] and repeatedly Terryfies it he creates the list [ 0,1,2,1,2,3,2,3,4,1,2,3,2,3,4,3,4,5,2,3,4, …]

What is the 2012^th number in this Terryfic list?

[Lời dịch]        Terry đã sáng tạo ra một phương thức mới để mở rộng một dãy số bất kỳ và đặt tên cho nó là Terryfy. Để tiến hành Terryfy dãy [1, 8] cậu ấy đã tạo thêm hai dãy mới là [2, 9] và [3, 10] bằng cách thêm 1 đơn vị cho mỗi phần tử trong dãy đứng trước nó, cuối cùng cậu ghép ba dãy vừa có thành một dãy mới là [1, 8, 2, 9, 3, 10] . Nếu Terry bắt đầu với dãy số đầu tiên là [0]  và thực hiện Terryfy nhiều lần để tạo ra dãy số [ 0,1,2,1,2,3,2,3,4,1,2,3,2,3,4,3,4,5,2,3,4, …]

Hỏi số thứ 2012 trong dãy số trên là bao nhiêu?

Hướng dẫn giải.

Nhận thấy số phần tử của dãy số sau mỗi lần Terryfy luôn được gấp 3 lần số phần từ trước đó.

Vậy ta có thể dễ dàng tìm được quy luật của số phần tử đi theo dãy như sau: 1, 3, 9, 27, 81, 243, 729 và 2187.

Vậy sau 7 bước dãy số của chúng ta sẽ có 2187 phần tử bằng cách ghép 3 nhóm 729 phần tử trước đó.

Gọi tn là số hạng đứng ở vị trí thứ n.

Vì 2012 = 729 + 729 + 554 nên ta suy ra t2012 = t554 + 2

Đồng thời 554 = 243 + 243 + 68 nên ta có được t2012 = t68 + 2 + 2.

Tiếp tục  68 = 27 + 27 + 14 nên ta có t2012 = t14 + 2 + 2 + 2.

Thực hiện các bước tương tự ta sẽ có t2012 = t1 + 1 + 1 + 1 + 2 + 2 + 2 = 0 + 1 + 1 + 1 + 2 + 2 + 2 = 9

Vậy số đứng ở vị trí thứ 2012 là số 9.

Hits: 6