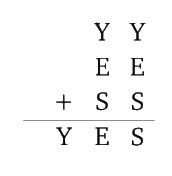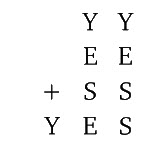Prepare for AMO 2019 – Grade 7 – Đề luyện thi toán tiếng anh AMO 2019 – Khối 7

Prepare for AMO 2019 – Grade 7

Week 1

Exercise 1. In the triangle shown, the first diagonal line, 1, 2, 3, 4 , …, begins at 1 and each number after the first is one larger than the previous number. The second diagonal line, 2, 4, 6, 8, …. begins at 2 and each number after the first is two larger than the previous number. The n^td diagonal line begins at n and each number after the first is n larger than the previous number. In which horizontal row does the number 2025 first appear?

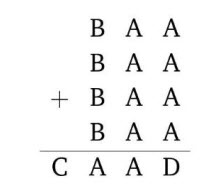
Exercise 2. In the puzzle (cryptarithm) below, each letter stands for the different digit. Find the sum A + B + C + D.

Exercise 3. Each of the integers 334 and 419 has digits whose product is 36. How many 3-digit positive integers have digits whose product is 36?

Exercise 4. For how many whole numbers from 5001 to 5499 does the product of the middle two digits exceed 6?

Exercise 5. In the following alphametic, different letters stand for different digits. Find the three digit sum YES.

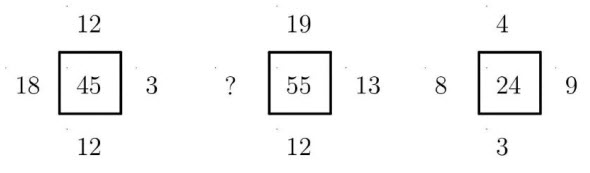
Exercise 6. Find the missing number.

Exercise 7. In the following cryptarithm, different letters stand for different digits.

Find the sum M + O + N + E + Y.

Exercise 8. There is a sequence of consecutive positive integers on the board. Exactly 52% of them are even numbers. How many odd numbers are there on the board?

Exercise 9. If the odd numbers are grouped in the following way:

{1}; {3, 5}; {7, 9, 11}: {13, 15, 17, 19}; …

what is the middle number in the 101^th group?

Week 2

Exercise 1. In the figure, AB = AC = AD. ∠ABC = 70°, and ∠ADC = 50°. Find the measure of ∠BAD.

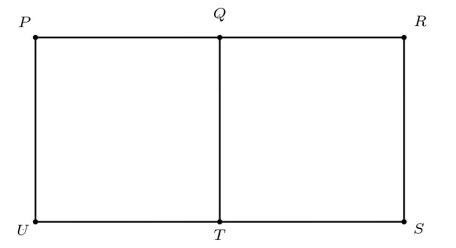
Exercise 2. The figure shows a rectangle PRSU with a line QT which divides the rectangle into two squares. How many right-angled triangles can be drawn using any three points P, Q, R, S, T, U as corners?

Exercise 3. In the diagram ST is parallel to UV. What is the value of x ?

Exercise 4. Tom and Jerry started with identical rectangular sheets of paper.

Each of them cut his sheet in half. Tom obtained two rectangles, each with a perimeter of 40cm

while Jerry obtained two rectangles 50cm, each with a perimeter of.

What was the perimeter of Tom’s original sheet of paper?

Exercise 5. In the following alphametic, different letters stand for different digits. Find the three digit sum YES.

Exercise 6. Find the missing number.

Exercise 7. In the following cryptarithm, different letters stand for different digits.

Find the sum M + O + N + E + Y.

Exercise 8. There is a sequence of consecutive positive integers on the board. Exactly 52% of them
are even numbers. How many odd numbers are there on the board?

Exercise 9. If the odd numbers are grouped in the following way:

{1}; {3,5}; {17,9, 11}; {13, 15, 17, 19}; …

what is the middle number in the 101^th group?

Week 3

Exercise 1. At a concert hall, a queue was formed at the box office before it opened at 1 p.m. From 1 p.m., a fixed number of people joined the queue every minute. There are 12 counters at the box office. If 7 counters are open, the queue can be cleared in 14 minutes. If 9 counters are open, the queue can be cleared in 10 minutes. If all 12 counters are open, how long does it take to clear the queue?

Exercise 2. A farming field can be ploughed by 6 tractors in 4 days. When 6 tractors work together, each of them ploughs 120 hectares a day. If two of the tractors were moved to another field, then the remaining 4 tractors could plough the same field in 5 days. How many hectares a day would one tractor plough then?

Exercise 3. Pump 4 can fill a tank of water in 5 hours. Pump B can fill the same tank in 8 hours.

How long does it take the two pumps working together to fill the tank?(round your answer to the nearest minute).

Exercise 4. To deliver an order on time, a company has to make 25 parts a day. After making 25 parts per day for 3 days, the company started to produce 5 more parts per day, and by the last day of work 100 more parts than planned were produced. Find how many parts the company made and how many days this took.

Exercise 5. One pump fills a tank two times as fast as another pump. If the pumps work together they fill the tank in 18 minutes. How long does it take the faster pump working alone to fill the tank?

Exercise 6. Four children have small toys. The first child has 1/10 of the toys, the second child has 12 more toys than the first, the third child has one more toy of what the first child has and the fourth child has double the third child. How many toys are there?

Exercise 7. In a Science lab, Sean takes 12 minutes to fill a cracked container completely with water. The crack will empty the completely-filled container in 60 minutes. Given that it takes x minutes to fill the container completely if there is no crack, find the value of x.

Exercise 8. A water tank, having the shape of a rectangular prism of base 100 square centimeters, is being filled at the rate of 1 liter per minute. Find the rate at which the height of the water in the water tank increases. Express your answer in centimeters per minute.

Exercise 9. Two different schools (A and B) have the same number of pupils. The ratio of the boys in school A and the boys in school B is 2 : 1 and the ratio of the girls in school A and the girls in school B is 4 : 5. Find the ratio of the girls in school A to the boys in school A.

Week 4

Exercise 1. In a primary school, 75% of the pupils play badminton, 70% play basketball and 65% play table tennis. Given that at least x% of the pupils play all three games, find the value of x.

Exercise 2. On a particular afternoon, Eugene and Benjamin left their school at the same time and headed towards the bus stop. After running at an average speed of 8 m/s for 30 second, Eugene ran past their classmate Dexter. Dexter was walking in the opposite direction the bus stop back to school, as he had left his pencil case in school. 20 seconds later, Benjamin walked past Dexter. Given that Benjamin was walking at an average speed of 1 m/s, find Dexter’s average speed in

Exercise 3. In a certain college, 40% of the senior class students are taking Physics, 30% are taking calculus and 10% are taking both. If 40 students are enrolled in the senior class, how many students are taking neither Physics nor calculus?

Exercise 4. In a lecture hall, there are 23 rows of seats. There are 12 seats in the first row. Each subsequent row has one more seat than the previous row. During an examination, there must be at least two empty seats between every two candidates in any row. What is the maximum number of candidates that the lecture hall can accommodate?

Exercise 5. A car travels from A to B at a speed of 40 mph then returns, using the same road, from B to A at a speed of 60 mph. What is the average speed for the round trip?

Exercise 6. Susan jogged from home to the sport complex at a constant speed of 6 km/h. 10 minutes later, her sister, Susie, started riding a bicycle along the same route towards the sports complex at a constant speed of 18 km/h. If they arrived at sports complex at the same time, how many seconds does it take Susan to jog from home to the sport complex?

Exercise 7. Mrs Wong made 25 boxes of pineapple tarts. On Saturday, she sold the pineapple tarts at $15 per box but realized that less than half of the pineapple tarts were sold. The next day, she reduced the price to $x per box, where x was a whole number. After selling all 25 boxes of pineapple tarts, Mrs Wong earned $280. Find the value of x.

Exercise 8. In a school 50% of the students are younger than 10, 1/20 are 10 years old and 1/10 are older than 10 but younger than 12, the remaining 70 students are 12 years or older. How many students are 10 years old?

Exercise 9. Brent travels from Point A to Point B downstream on a motorboat. If he switches on the engine, he will take 5 minutes to reach Point B. If he switches off the engine, he will take 15 minutes to reach the Point B. Given that it takes x minutes for Brent to travel from Point B to Point A with engine switched on, find the value of x.

 

Hits: 34